1. 프랙탈 기하학에 대한 개념과 고찰

프랙탈(Fractal)이란 말은 ‘부서지다’라는 라틴어 동사 ‘frangere’에서 파생한 부서진 상태를 뜻하는 형용사인 ‘fractus’에서 유래되었다(Lee & Jang, 2008). 수학자 베노이트 만델브 로트(Benoit Mande lbrot, 1924-2010)가 ‘불규칙한 형상의 집합’을 정의하기 위하여 처음 사용한 언어이다(Gleick James, 2013).

프랙탈은 자연에서 흔히 볼 수 있는 불규칙하고 무정형한 모양들을 가르키는 겉으로 보기에는 복잡하고 무질서해 보이나 그 안에 규칙을 내포하고 있음을 설명한다(An, 2013). 즉, 프랙탈 기하학은 지금까지 사용해 온 규칙적인 모양이나 곡선, 곡면으로 인식할 수 없는 자연의 복잡한 모양과 형상에 대해 밝히고, 전체와 부분의 유사성을 만들어 내는 객관적인 방법을 연구하며, 그 속에 숨어있는 새로운 규칙들을 찾아내고자 하는 학문이다(Kim, 2011). 무질서해 보이는 자연의 복잡성 안에 숨어있는 공통적인 질서와 규칙은 과학의 발달로 수치가 가능해지면서 자연에서 찾은 패턴을 인식하게 되었다(Shin, 2022). 이러한 불규칙한 모양 속에 내재되어 있는 연속적인 유사성을 프랙탈이라 하며, 프랙탈 기하학은 자연의 복잡한 현상과 형태를 밝히는 개념으로써 전체와 부분에 내재하는 유사한 패턴을 만들어 내는 객관적인 규칙을 말한다(Kim, 2017). Noh(2010)의 연구에서 프랙탈 기하학은 끊임없이 연속적이고 자기 유사적인 구불구불하게 휘몰아치는 디테일을 보여주는 수학적인 모습들이라고 하였다. 프랙탈은 자연의 형태를 보여주는 자연의 기하학이며(Jung et al., 2017). 무정형하고 불규칙적인 자연의 모양이다. 우리 인체 곳곳에 숨어 있는 프랙탈 구조는 자연과 닮았고, 인간과 동물의 혈관 분포와 산맥, 구름, 해안선, 나뭇가지 등 자연에서 수많은 프랙탈 기하학의 구조를 나타내고 있다.

수학적 용어로서의 프랙탈은 전체적으로 큰 형태를 부분으로 보았을 때 그 안에서 전체의 모습을 가지고 있는 무한한 형태의 기하학 도형을 일컫는다. Kim(2000)의 연구에서는 프랙탈 기하학은 자기 유사성, 비선형성, 불규칙성, 무작위성, 자기 조직성, 반복성, 응집성 등의 특성을 나타낸다고 하였으며, 프랙탈의 특징은 프랙탈 차원을 갖음과 자기 닮음이라고 하였다(Kim & Kim, 1998). 또한, Kim(2011)의 옵티컬 패턴의 주얼리 디자인 연구에서는 프랙탈 기하학의 조형 원리는 중첩, 반복, 왜곡, 스케일링의 변환이라고 하였으며, Kim(2003)의 연구에 의하면 만델 브로트에 의해 제안된 프랙탈은 자연계의 구조적인 비규칙성을 기술하고 분석할 수 있는 새로운 기하학이라고 하였으며, 만델 브로트는 자연의 복잡한 형상과 불규칙한 패턴의 연구에서 나타난 공통적인 특성을 자기 유사성(Lee, 2003)으로 보았으며, 자연 현상을 해석하는 강력한 도구로 설명했다. 프랙탈은 무한히 작은 축적에 이르기까지 자기유사성을 갖는 비정수 차원의 복잡한 기하학적 물체라고 언급하였다(Kim, 2003).

이와 같이 프랙탈 기하학은 함수와 변수, 함수 되부름 등을 활용한 일종의 수학적 코드이다(You & Young, 2001). 프랙탈의 다양한 특성은 상호 연결되어 있음으로, 본 연구에서는 프랙탈 기하학의 구성원리의 자기유사성과 비선형성, 불규칙성, 무작위성과 조형원리의 중첩성, 반복성, 왜곡성과 스케일링의 변환을 중심으로 살펴보고자 한다.

2. 프랙탈 기하학의 조형적 구성 원리

2) 무작위성, 비선형성, 불규칙성

프랙탈의 무작위성(Randomness)은 프랙탈 패턴이 무작위성을 결합하여 생성되는 현상을 말한다. 이는 완전히 예측할 수 없는 형태의 프랙탈을 만들어 내는 것을 의미하고, 프랙탈의 일부 구성 요소는 무작위적으로 선택되거나 변형되어 전체적인 형태가 결정된다.

무작위적인 프랙탈은 복잡한 세계 구조를 가질 뿐만 아니라, 실질 세계에 존재하는 비예측성도 가지고 있다(Kim, 2003). 반복, 점진, 척도를 불규칙적이고 우연으로 선택함으로써 해안선, 산맥, 행성 같은 것들을 영화나 비디오 각종 광고에서도 쓰일만큼 진짜처럼 보이도록 만들 수 있다(John Briggs & David Feet, 1990). 무작위성은 예측할 수 없는 복잡성과 재미있는 시각적인 패턴을 제공하기 때문에 예술, 컴퓨터 그래픽, 시뮬레이션, 자연현상 모델링 등 다양한 분야에서 사용될 수 있다. 프랙탈은 비선형적인 특성을 가지고 작은 요소들의 조합으로 이루어진 복잡한 패턴을 보이는 것이 특징이며, 선형적인 기하학에서는 단순한 기하학적 변환만으로 모양이 변하지만, 프랙탈에서는 비선형적인 변화가 중요한 역할을 한다.

비선형성(Nonlinearity)을 나타낸 뉴턴의 방정식에서는 작은 변화로 작은 효과를 얻고, 큰 변화로 큰 효과를 얻기 때문에 선형(Linear)이라는 용어를 쓴다(Kim, 2002). 이렇게 변수의 값에 따라 비례적으로 크거나 작아지는 방정식을 선형이라고 한다. 비선형계에서의 특징은 압력의 작은 것이 변환되어 예측하지 못한 큰 변화를 일으키는 현상이며, 초기 조건에 대한 민감한 의존성이며 이런 경우를 기상학계에서는 나비효과라고 부른다(Kim, 2011).

불규칙성(Irregularity)은 자연현상의 규칙적인 불규칙성을 의미한다. 예를 들면 뒤틀린 나무의 형상, 불규칙한 생강 뿌리, 선인장, 화성암의 거품 등은 다양한 형태가 반복되면서 불규칙하게 배열되어 있다(Yun, 2012). 이러한 현상이 바로 프랙탈의 불규칙성이며 이는 패턴의 반복과 변형으로 공간을 역동적으로 만든다(Song, 2006).

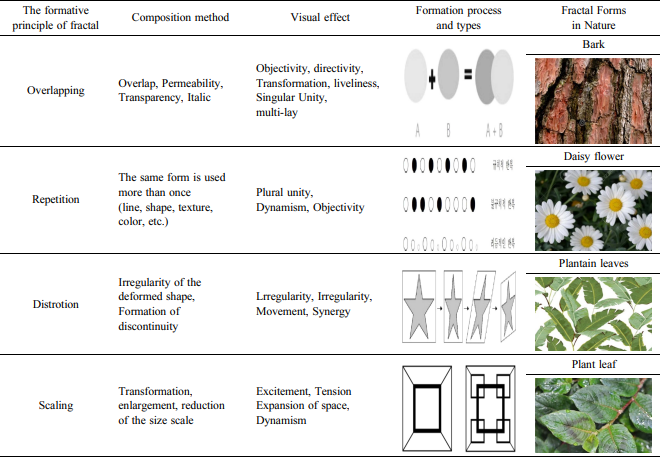
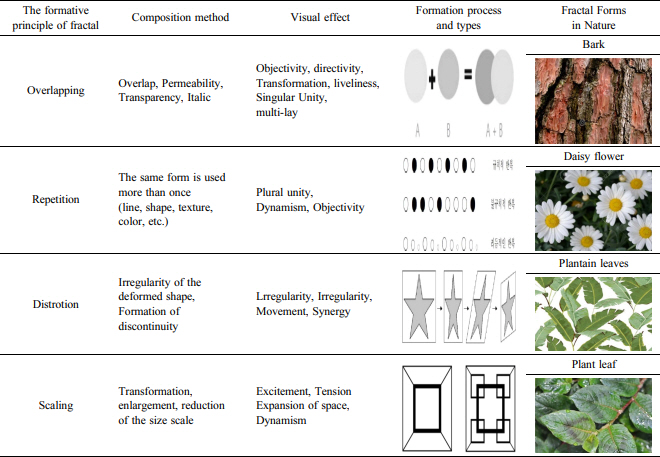
결론적으로 프랙탈 구조는 무한하게 세분이 가능한 패턴 안의 패턴이 자기유사성과 비선형적인 프랙탈 차원을 가지며, 생성의 출발점에서부터 확산하여 다양한 형태가 반복·축소·왜곡·변형된 구조를 이룬다(Yun, 2012). 프랙탈 도형은 종종 컴퓨터 소프트웨어를 이용한 재귀적이거나 반복적인 작업에 의한 패턴으로 만들어진다(Eom & Jeong, 2012). 프랙탈 기하학의 구성원리의 형태적 특성의 개념, 자연에서 나타나는 프랙탈 이미지를 정리하면 Table 1과 같이 정리된다.

Table 1.

Classification of Shape Characteristics and Compositional Principles of Fractal Geometry

3. 프랙탈 기하학의 디자인 조형 원리

4) 스케일링(Scaling)의 변환

스케일링의 방법은 프랑스의 수학자 베노이트 만델브로트(Benoit Mande lbrot)의 프랙탈 개념이 차용된 것(Kim, 2011)으로서, 프랙탈 패턴을 특정 비율로 확대 또는 축소하는 변환을 의미한다. 이로 인해 프랙탈 패턴이 다양한 크기로 변화하며, 반복적인 구조를 더 자세히 또는 더 넓게 관찰할 수 있다.

스케일링은 프랙탈의 특성을 더 잘 이해하고 시각화하는 데에 매우 유용하다. 스케일링을 통해 프랙탈 패턴이 다양한 크기와 미묘한 세부 사항을 갖는 것을 관찰함으로써 프랙탈의 자기유사성과 반복적인 구조를 확인할 수 있고, 또한, 스케일링은 프랙탈 기하학 디자인에서 시각적인 다양성과 창의성을 높이는 분야에 사용된다. 예를 들어, 컴퓨터 그래픽스에서는 객체의 크기를 조절하여 3D 모델을 확대 또는 축소하여 다양한 시각적 효과를 얻을 수 있고, 데이터 시각화에서도 스케일링을 사용하여 차트나 그래프의 크기를 조정하여 데이터를 더 명확하게 보여줄 수 있다. 스케일링은 이미지 처리, 컴퓨터 비전, 게임 개발 등 다양한 분야에서도 사용되는 중요한 변환 기법이다. 프랙탈 기하학 디자인의 조형 원리의 특성 구분과 시각적 효과는 Table 2와 같이 정리된다.

Table 2.

Classification of Formative Principles of Fractal Geometry Design

4. UV 젤 네일아트

네일아트는 21세기 뷰티산업의 발전 속에서 대중들의 관심과 아름다움을 추구하는 욕구 표현 방식의 수단이 되고 있다. 그중에서도 UV 젤 테크닉은 인조 네일의 가장 현대적으로 강화된 기술이고, 네일아트는 손톱이라는 작은 공간에 표현하는 예술 영역으로 개성과 이미지를 표출하는 수단으로 대중화됨에 따라 현대 여성들의 큰 관심사가 되고 있다(Shin, 2014).

네일아트 디자인은 네일리스트의 내면적 이미지를 독창적이고 창의적인 디자인과 함께 다양한 소재와 표현기법으로 장식하여 미의 세계를 시각적으로 표현하는 영역이다(Choi, 2000). 또한, 요즘 시대에는 표현예술의 한 분야로서 영역 확대가 이루어지고 있으며 토털 패션의 한 부분으로 중요한 역할을 하고 있다. 특히 컬러 젤의 산업발전으로 기존 발색이 잘 되지 않고 아세톤에 녹지 않는 제품에서 지금은 다양한 컬러의 제품개발이 많이 이루어지고 있다. 최근에는 고객들이 먼저 인터넷 등 다양한 매체를 통하여 디자인을 쉽게 접하고 네일아트 디자인에 대한 지식 및 수준이 향상되어 고객들의 요구를 만족시킬 수 있는 창조적인 네일 디자인 개발이 필요하게 되었다(Bae, 2015). 이와 함께 미술작품에 사용되는 모든 도구와 네일아트에 사용되는 소품들이 만나 예술적 작품으로써의 우수한 네일아트 디자인이 완성되었다. 네일 디자인은 개개인의 독특한 개성을 표현해 줄 수 있는 흥미로운 작업으로 특히, 젤은 UV 램프에 큐어링 하기 전까지 자유롭게 사용할 수 있어 시간적인 제한을 받지 않고, 이러한 장점을 이용한 네일아트 기법으로는 젤 아트, 스톤 아트, 오브제 아트, 데칼 아트, 워터 데칼 아트, 마블 아트, 핸드페인팅, 포크 아트, 에어 브러쉬, 엠보 아트, 3D 아트, 컬러 아트, 디자인 스캅춰 등이(Kim & Kim, 2023)있고, 다양한 방식으로 아트를 표현할 수 있다. 네일아트 기법 중 핸드페인팅(Hand Painting)은 조형 요소인 점, 선, 면과 색상을 잘 고려하여 풍경이나 꽃, 동물, 사물, 케릭터 등을 섬세하게 터치하여 예술적인 디자인을 창조적으로 표현할 수 있다. 또한, 여러 가지 브러시 종류로 디자인의 표현을 달리할 수 있으며 물감과 물의 농도에 따라 선명한 이미지와 명암을 나타낼 수 있다(Kwon, 2013). 핸드페인팅은 상징적인 표현과 사실적인 회화 묘사 등 다채로운 표현이 가능하며 색상과 디자인을 자유롭게 구사할 수 있어 네일 위에 펼져지는 아름다운 예술이라 할 수 있다(Ko, 2020).

1. 연구범위

자연은 디자인에 있어 아름다움의 근원이며 조형 요소와 원리가 모두 조합된 표현 대상으로 볼 수 있다(Kim & Kim, 2018). 자연 속에서 찾아낸 프랙탈 기하학의 조형적 특징은 디자인에 있어서 미적 근거를 탐색하는데 매우 중요한 원리가 된다. 자연의 형태구조에서 찾아낸 가하학 패턴과 형태원리를 기본으로 한 디자인은 합리적 구조에 대한 방법적 합리성과 과학적 유용성을 동시에 가질 수 있고, 이는, 네일아트 디자인에 있어 의미있는 시도가 될 수 있다고 본다.

본 연구의 범위는 자연의 유기적인 형태들에 나타나는 프랙탈 기하학적 형태의 고찰을 통해 화화 작품에 나타난 과학적 이론인 프랙탈 기하학의 조형적 특성 이미지를 네일아트 디자인에 적용하는 것이다. 이에 따라, 회화작품에 내재하여 있는 프랙탈 특성을 고찰하여 미용 예술과 과학의 통합체로서 융합 디자인을 개발하였으며, 실질적인 디자인을 통한 제작과정을 보여주었다. 프랙탈의 조형적 구성원리와 디자인 조형 원리의 분석을 통해 프랙탈에서 얻어낼 수 있는 예술적 아름다움을 표현하여 실질적으로 네일아트 디자인에 적용하여 제시하였다.

2. 작품제작

본 연구의 구체적인 작품제작 방법은 프랙탈 기하학에 기초하여 과학과 디자인의 접목의 시도를 위해 프랙탈 기하학의 특성을 선행연구 및 전문서적을 고찰하였다. 프랙탈 기하학적 형태의 화예 디자인 조형 작품에 관한 연구(Nam, 2002), 프랙탈 기하학의 조형성을 응용한 헤어아트 연구(Lee, 2015), 해체주의 건축과 패션에 나타난 조형성 및 색채 특성 비교분석(Lee et al., 2014)의 연구에서는 자기유사성, 비선형성, 불규칙성, 무작위성, 자기조직성, 비예측성으로 구성원리의 특성을 연구 분석하였고, 프랙털 기하학에 근거한 텍스타일 디자인 연구(Song, 2006), 프랙탈적 해석에 의한 텍스타일 디자인 응용 가능성에 대한 연구(Yang, 2000)에서는 디자인 조형원리의 분석으로 중첩성, 반복성, 왜곡성, 스케일링 변환의 특성으로 분류하였다.

이를 토대로 본 연구에서는 회화작품에 내재하여 있는 프랙탈 기하학의 구성원리 특성의 자기유사성, 불규칙성, 비선형성과 프랙탈 디자인 조형 원리에서 많이 사용 되는 중첩성, 반복성 5가지로 분류하고, 회화작품 속에 표현된 프랙탈의 특성을 네일아트 디자인에 실질적으로 표현해 보고자 한다.

작품제작은 선행연구를 토대로 회화작품에 표현된 프랙탈 기하학의 특성이 나타난 1. 자기유사성은 바실리 칸딘스키의 ‘원안에 원’, 작품, 2. 불규칙성은 파블로 피카소의 ‘아비뇽의 처녀들’ 작품, 3. 비선형성은 빅토르 바자렐리의 ‘얼룩말’ 작품, 4. 중첩성은 마르셀 뒤샹의 ‘계단을 내려오는 누드 NO₂’ 작품, 5. 반복성은 모리츠 코르넬리스 에셔의 ‘Metamorphosis I’의 5가지 작품을 선택하여, 각 작품이 표현되는 프랙탈 기하학의 특성을 응용하여 총 5점의 작품을 제작하고자 한다.

작품제작과정으로 회화작품의 프랙탈 기하학의 특성을 충분히 파악한 후 종이에 색연필로 1차 디자인 스케치를 하고, 그 위에 2차로 핸드페인팅 기법을 이용하여 젤로 표현해 보았으며 그 후 아트용 팁 위에 작품을 제작하였다. 기기와 재료는 내츄럴 커브 아트용 네일 팁, 베이스 젤(Base Gel), 탑 젤(Top Gel), 젤 브러시(Gel Blush), 핸드페인팅 라인 젤(Hand painting Gel), UV/LED 겸용 젤 램프(UV/LED Gel Lamp)을 이용한 재료와 기구는 Table 3과 같고, 정교하게 핸드페인팅 아트로 작품 제작 표는 Table 3과 같고, 작품작업 계획은 Table 4와 같다.

Table 3.

Material and Instrument

Table 4.

Work Design Plan

1. 자기유사성(Self-similarity)

작품 I은 프랙탈 기하학의 자기유사성을 나타내는 바실리 칸딘스키의 ‘원안에 원’이다. 자기유사성은 모든 축척을 관통하는 대칭성이고, 이것은 회귀(Recursion) 즉, ‘패턴 안의 패턴’을 의미한다(Yang, 2000). 즉, 규모가 점점 작아지는 방향으로 상세한 모양이 반복되는 것을 의미하기도 하며, 이러한 자기유사성은 프랙탈의 기초를 이루고 있으며 이 특성을 엄격하게 지키는 것이 있는가 하면 약간의 변화를 하는 것도 있다(Kim. 2003). 세부 구조를 확대해 보면 부분이 전체 구조와 자기 닮음 형태를 보이는 자기유사적인 특성을 갖는다. 이와 같은 자기유사성이 나타난 바실리 칸딘스키의 작품 ‘원 안의 원’은 기하학적인 도형과 선의 중첩으로 프랙탈 기하학의 특성을 작품 I에 디자인을 표현해 보았다. 네일아트 이미지 표현은 Table 5와 같다.

Table 5.

Self-similarity - Wassily Kandinsky ‘One in a circle’

2. 불규칙성(Irregularity)

예술가에게 있어 불규칙성(Irregularity)은 필수 불가결의 요소이다. 위대한 예술 작품에는 고전적인 형태 속에서도 규칙의 평정함 속에 혼돈의 힘이 항상 나타나 있기 마련인데, 모든 위대한 예술은 질서와 혼돈의 성장, 정체의 팽팽한 긴장을 추구한다(Song, 2006). 작품 II는 파블로 피카소의 ‘아비뇽의 처녀들’이다. 아비뇽의 처녀들은 프랙탈 기하학의 특성 중 규칙에서 벗어난 상태를 의미하고, 혼란스러워 보이지만 그 내면에서는 질서를 내포하고 있는 특성인 불규칙성을 말한다. 이차원적인 평면에 하나의 형체를 삼차원의 세계인 듯 여러 각도로 표현해 혼란스러운 시각으로 프랙탈의 모습을 볼 수 있다. 형태가 끊임없이 반복되면서 불규칙하게 배열되는 성질을 가지고 있다. 이를 바탕으로 불규칙성이 표현된 ‘아비뇽의 처녀들’ 작품을 네일팁에 적용하여 작품 II에 디자인을 표현해 보았다. 네일아트 이미지 표현은 Table 6과 같다.

Table 6.

Irregularities - Pablo Picasso's ‘The Maids of Avignon’

3. 비선형성(Nonlinearity)

뉴턴의 작은 변화에 따른 작은 효과, 큰 변화에 따른 큰 효과를 가져오는 선형(Linear)적인 방정식에 반하여, 비선형성(Nonlinearity)의 특징은 입력한 작은 변수에 의해 변환의 과정을 거쳐 최종 출력되는 결과는 초기에 예측할 수 없는 큰 변화를 가져오는 현상을 뜻하며, 이를 기상학에서는 나비효과라고 부른다(Lee, 2015). 비선형성의 사례를 살펴보면 초기 조건에서 변화를 거듭함에 따라 스케일의 확장 및 왜곡된 반복이 이어져 구조를 예측할 수 없는 형태 변화로 화산폭발로 인해 쌓여가는 용암 주름, 흐르는 계곡물의 방향, 당구대의 공이 굴러가는 방향 등으로 설명될 수 있다. 빅토르 바자렐리의 ‘얼룩말’ 또한 의도적인 이미지를 위해 어색한 모습과 이상스럽게 뒤틀리고 왜곡된 파격적인 비례로 묘사하기도 하면서 새로운 미를 창조해 나갔다(Jo, 1997). 비선형성의 특징을 바탕으로 Black, White, Sky blue 3가지 컬러를 가지고 작품에 표현해 보았다. 네일아트 이미지 표현은 Table 7과 같다.

Table 7.

Nonlinearity - Victor Vazarelli ‘Zebra’

4. 중첩성(Nesting)

작품 III는 중첩요소에서 가장 기본적이고 중요한 것은 선적인 요소, 즉 축이 되는 선인데 축의 중첩은 중첩성의 표현방법 중 가장 대표적인 것이다(Lee, 2014). 여러 단계의 층들이 겹침, 혹은 포개어짐을 통하여 이루어지는 중첩성을 표현해 보았다. 화산활동 지형에서 흔히 나타나는 주상절리의 사례를 통해 쉽게 파악할 수 있고, 비슷한 형태의 기둥들이 쌓여 하나의 덩어리를 이루고 있다. 마르셀 뒤샹의 ‘계단을 내려오는 누드 NO 2’에서는 서로 다른 형태가 포개어져 깊이감이 생김으로써 공간의 착시를 일으키는 중첩과 반복을 통해 프랙탈이 나타난다. 사람의 움직임의 모습을 연속적으로 묘사한 그림으로서 프랙탈의 중첩성을 잘 표현한 작품이다. 프랙탈 기하학의 중첩성이 드러난 ‘계단을 내려오는 누드 NO 2’를 작품 III에 디자인을 표현해 보았다. 네일아트 이미지 표현은 Table 8과 같다.

Table 8.

Overlapping - Marcel Duchamp ‘Nude Descending the Staircase NO 2’

5. 반복성(Repetition)

작품 V는 프랙탈 기하학의 반복성을 잘 보여주는 모리츠 코르넬리스 에셔의 ‘Metamo rphosis I’ 작품이다. 반복(Repetition)이란 점과 점 사이에는 점이, 선과 선 사이에는 선이, 형태와 형태 사이에는 형태가, 공간과 공간 사이에서는 공간이, 사건과 사건 사이에는 사건 이 동일한 패턴이 연속되어 가는 것을 말한다(Nam, 2002). 모리츠 코르넬리스 에셔의 작품에서는 공간의 간격에 의하여 반복이 생겨 동일한 패턴이 연속된다. 이는, 복잡한 구조 속에 되풀이되는 비슷한 요소들의 반복으로 다양한 형태를 얻는 것을 말한다. 반복은 통일을 위한 중요한 수단이기도 하고, 미의 구성 원리 중 반복은 가장 기본적인 원리로 디자인에 우선시 된다(Yoo, 1963). 디자인 스케치를 통해 동일한 패턴의 반복을 작품 Ⅴ에 디자인을 정교하게 표현해 보았다. 네일아트 이미지 표현은 Table 9와 같다.

Table 9.

Repeatability - Moritz Cornelis Escher ‘Metamorphosis I’